
This material is relevant to the discussion on
www.ma.umist.ac.uk/avb/wherefrom.html
of `Where will the next generation of UK mathematicians come from?', and
is linked from the pages there. Other relevant material is on my list of
articles on teaching and popularisation, particularly
the articles on methodology and on
context.
The basic question is also not `where from?' but `why?'. Why should students go into research mathematics if the spirit of research mathematics is not conveyed to them as undergraduates, and in any case the spirit of free enquiry is shackled by the necessity to bring in research funds and to assuage Research Assessments Exercises, which work on on undisclosed and unverified mode of assessments? and assessment of what? It seems to be all about standardisation, the removal of orginality, and innovation, following someone else, not encouraging new lines in the UK. And the resulting verdict allows for no discussion, no appeal. A view among radical medics is that `diagnosis without treatment is unethical'. See further discussion on the notion of quality, and also a quotation on the role of imagination in poetry.
This article is an edited web version (with further minor editing for clarity,
and adding and updating links, done on July 4, 18, 2005) of the article published
in:
Mathematics education as a research domain: a search for identity,
ed. Kilpatrick, J. and Sierpinska, A., Kluwer, Lancaster (1997) 459-476.
This is the volume resulting from the conference for the
ICMI
study on What is Research in Mathematics Education, and What Are Its
Results?, held at the University of Maryland in College Park, Maryland,
USA, 8-11 May 1994. It was attended by 81 participants from 23 different
countries. There were two chosen representatives of the research mathematics
community at the ICMI meeting, Lenore Blum, Deputy Director of MSRI, Berkeley,
from the USA, and myself, from Europe.
One morning was given to talks and discussions in the National Science Foundation in Washington. Lenore Blum gave a talk, and this paper developed from the talk I gave.
I had hoped to write an overall view of output as suggested by the title, but this turned out to be too ambitious an undertaking.
I am also conscious that a good deal of the readership for this article will be people who have had experience of teaching in schools, of teaching the teachers over many years, and who are well aware of the work that has been done in mathematical education. It seems advisable therefore to talk about the areas in which I have had experience, and leave the readers to debate the possible analogies and relevance to wider issues.
The use of the word ``should" in the title is normative, and might suggest that I think I know all the answers. To the contrary, what I hope this article will do is direct attention to some interesting questions.
The question of "output" is not a bad place to start in considering an activity. The quality of mathematics education is an important issue for the future social and economic strengths of our countries. We are also all interested, for example as taxpayers, in the output of activities which are publicly funded. How should we judge this? Can we give reasonable expectations for research in mathematical education if we do not know what we can reasonably want from mathematical education itself? Otherwise, it might even be suggested that an aim of a conference on mathematical education is to improve the status of the research and the researchers.
In discussing "output" I am going to start at the ``top" end, namely that of research in mathematics. This may at first seem foolish, since any comprehension of what goes on in research in mathematics is generally thought to be way beyond the needs and comprehension of the vast majority of those who go through the educational process.
Against this I would set the argument that it would be desirable for there to be a clearer view in mathematical education as the nature of the mathematical beast, in order to know how to deal with it. If it is unclear as to what is mathematics, and what are its main achievements, what constitutes performance in it, then what is the hope of teaching it in a clear way, of coming up with new practical hints as to how it should be taught more effectively? I wondered after attending ICMI94 whether this itself was not the crucial unasked question, which required debate. Indeed, one speaker did refer to the paucity of practical hints for teachers which were available. It is more difficult to give practical hints for teaching an activity not itself well defined. Not all the resources of psychology, linguistics, or philosophy, will help education and training in the sport of, let us invent one, say, Yarangoo, if the rules of Yarangoo, and the method by which one wins a game of Yarangoo, are not understood in the first place. For this, it does not matter whether the aim is that of a beginner or a first division player.
I find some support for this view from articles I recently came across in Mathematics Teaching, December, 1986, "Special Issue: The roots of mathematical activity". Raffaella Borasi writes that:
Several recent research studies investigating the difficulties that many students encounter in learning mathematics have suggested that what students believe to be the nature of mathematics may influence considerably their possibilities for success in the subject.
Phil Boorman in the same issue explains how his outlook on teaching mathematics is shaped by his view of mathematics as the study of pattern and structure:
Now, if I am right in defining mathematics in this way, everyone is very, very good at `doing' mathematics - if they were not they would be dead - for all thought is mathematical.
Here is another example of how a view of mathematics can affect teaching and assessment. A colleague in London, say Fred, tells the story of how his son, say Bob, was given as an investigation the problem of determining the number of diagonals of a regular polygon. Bob and two friends came in one day when Fred was watching television and started discussing the problem. They tried a few low dimensional cases, came up with a general formula, tested it out for pentagons, saw they had got it wrong and needed to divide by two, and so arrived at the correct formula. Fred was delighted with their progress. The teacher was not so delighted. One of the boys just wrote down the answer and got 0. It appeared they were supposed to write a nine page project, testing special cases, drawing graphs, and so on. As the teacher explained: ``They had to learn: there is more to mathematics than just thinking." None of this had been explained before they started the project.
Since the ICMI94 was broad in the areas of study which were used to try and illuminate the question of what should be research in mathematical education, it is right that mathematics itself, what it advances towards, and the way it advances, should have some pride of place. Otherwise, we might have Hamlet without the prince.
A further point is the psychological truism that the behaviour of people is more similar if they are compared at the limits of their ability. The struggles that we have to understand and master advanced new ideas could give some sympathy for those who are also struggling at a much lower level of performance, and perhaps suggest some help in ways of improving this performance.
An advantage of the research viewpoint is that it counters the following
assumption:
there is always a ``right" mathematics, and the problem is to get people
to behave in the way assumed by this mathematics.
To the contrary, from the research point of view, we are especially interested in those parts of mathematics where we feel uncomfortable, since this feeling could be a pointer to a different approach being required. It is easy to forget the way in which was once research becomes, maybe over centuries, part of everyday mathematics, and so a part of mathematics teaching. Sometimes mathematics teaching is forced into the latest view of "modern" mathematics, to its detriment. Views even on basic mathematics are changing, partly in response to research needs and the developing language to describe new kinds of structures, and the ways in which structures interact, but also in response to new understandings of what mathematics is about and how it works.
David Tall in the abstract of his ICMI lecture at the ICM Zurich, 1994, writes:
There is thus a significant difference between the flexible thinking of the mathematician and the form in which the product of that thought is eventually communicated.
One of the ways mathematics progresses is in the closing of this gap, by finding forms, structures and languages in which the way we think can be more properly, more accurately, and more understandably expressed, and even more importantly, can yield new ways of thinking about a topic. These new forms then allow for more elaborate patterns of thought, calculation, and deduction. For example, mathematics was held up for centuries for lack of the ``trivial" concept of zero. (I owe this point in this context to A. Grothendieck, the twentieth century master of the development of concepts.) Were children once beaten for not being able to add properly in Roman numerals?
As an example, a striking change in basic thinking in mathematics is the existence of a move away from set theory as a ``foundation" for mathematics, and a realisation that a more flexible and intuitive approach is needed. The tools for this move are provided by category theory. In this method, emphasis is placed not on set theory, and not on the "elements" of a set, since these are somewhat counte rintuitive when one comes to large sets, such as the real numbers. Instead, emphasis is on the functions, and so on the relations between structures, through the homomorphisms between them. The constructions that can be made on objects are defined by the relations of these constructions to all other objects. In this view, functions return somewhat to their more intuitive role, rather than the passive role as a set of ordered pairs, a logical device as part of a thrust to give mathematics a ``safe" foundation.
Thus the difficulties which pupils, students, and professors have, and will always have, in learning concepts, procedures, and skills, in mathematics, is one aspect of a process with two variables, the learner and the mathematics. The processes of teaching, and so of trying to understand in order to explain to others, has often been a stimulus to the development of mathematics. It would be fascinating if philosophy and the social sciences of education, linguistics, and psychology, which figured so much in the discussions at ICMI94, can help in this process.
It is regrettable that the importance, for the progress of science and mathematics, of good exposition, of revealing underlying beauties, as a foundation for the future, is little understood in research assessments. There is a difference between `advancement of knowledge' and `advancement of understanding'. Yet the latter is often a motivation for young people to study mathematics at various levels.
The output of research in mathematics
It could be surprising to you that there might be any question about this. However the public and Government are in general unclear as to what mathematicians produce and how valuable is what they produce. Mathematics undergraduates, even very able ones, are often unclear that any research goes on in mathematics. This is not surprising since they are usually not required to look at original papers, nor to acquire any understanding of current work in progress.
Whereas astronomers, physicists, biologists, engineers, chemists, and so on, have worked hard to convince the public and Government as to what they are doing, and what constitutes a significant advance, it is less clear that this has happened in mathematics. The biggest splash recently has been for the solution of Fermat's last theorem. Thus the solution of famous problems is often advertised as the main success of mathematics, and this view is encouraged by mathematicians. Certainly the solution of such problems will bring fame within mathematics to the solver. What will be the effect on science, technology and the general public?
The history of mathematics shows that the contribution of mathematics to science and technology has been to provide a precise and developing language for the invention, representation, and discussion of certain concepts and relationships, together with a mode of deduction, calculation with and exploration of these. Mathematics has been able to say, in places where it can be applied: This is true, and that is false. This has enabled mathematics to reveal astonishing elaboration of patterns and structure, to provide tools for applying these structures, and to show new problems. The fact that mathematics is, if you like, the science, craft, and art, of pattern and structure, explains why it underlies so many other scientific and technical areas, which are themselves seeking to understand the patterns and structures in nature. We should avoid, though, the idea that the interest of mathematics rests on these applications, rather than the joy of the investigation itself. Indeed, some of the structures which have been forced on mathematicians by the logic of their arguments, and which have seemed weird and strange, have later, sometimes many years later, found their true place in applications. A good example is the theory of fractals, and of chaos.
Within mathematics there has long been a need to decide what is good mathematics. This occurs most crucially at the sharp end of publication. Authors have to decide for which journal their work is good enough. Referees and editors of journals have to decide whether or not a submitted paper should be accepted, and while competition for space in the "top" journals continues to increase, this decision has to be made on the basis of which are the "best" papers. Yet the question of what is good mathematics is little debated at the professional level, and an understanding of this is not explicitly part of a qualification for an undergraduate degree or even postgraduate. By contrast, students of, say, design, or musical performance, are introduced to this question as a basic object of their studies.
To give some focus to these questions, I would like to give some account of what I have been doing mathematically for the last thirty years. In any case, I like explaining this background, and the way this research has gone has influenced my views on mathematics as a whole. There has been a "reach for the stars" aspect of this research, and it has been satisfying that some basic foundations of this route have now been firmly laid down.
After my PhD in topology, not so sure of the direction I wished to go, I embarked, as a kind of displacement activity, on writing a topology text. Its principal aim was to explain the main basic results in algebraic topology, particularly the notion of a cell complex as a way of representing a space as constructed out of ``nice" and comprehensible bits, namely the ``cells" or ``balls", and the use of the so called fundamental group as a topological invariant.
A crucial part of this theory is the calculation of the fundamental group, in which a main tool is what is known as the Van Kampen theorem, first found in the mid 1930's. It shows how the fundamental group of a big space can be obtained if the space is the union of two ``nice" parts, such that the fundamental groups of these parts, and of their intersection, is known. However, to use this theorem, the intersection of the parts has to be connected, to have only one ``piece", and this prevented the theorem from being used to calculate the fundamental group of a basic example of a space, the circle, where the result is the additive group of integers. This example had to be determined by another method, the use of the exponential function from the real line to the circle, which wraps the line around and around the circle, like a rope around a bollard. Of course, this wrapping method is a nice, intuitive, and important method, but I still found the diversion unaesthetic.
In 1965 I came across a 1964 paper of Philip Higgins on the applications of groupoids to group theory. The notion of groupoid was introduced by Brandt in 1926, as a tool for extending important work of Gauss on the composition of quadratic forms, from the case of two variables to that of four variables. A groupoid should be thought of as a group in which the multiplication is not everywhere defined, so that many identities are allowed. Intuitively, the notion of groupoid corresponds to that of travelling between many points, so that a journey from London to New York can be composed with one from New York to Tokyo, but not with one from Washington to Montreal. By contrast, with a group, you always return to the starting point. (The word groupoid is, unfortunately, also used for the quite different notion of a set with a binary operation.)
The notion of groupoid was found in topology as the fundamental groupoid. It was recognised in the 1950s that groupoids gave a nice account of one aspect of the theory, that of change of base point. Perhaps this aesthetic feature should earlier have been taken as a clue that something potentially important was going on. However, groupoids were regarded as something of a curiosity, since the real interest was felt to be in the widely used notion of abstract group, recognised as one of the central concepts of mathematics.
To my surprise, I found in 1965 that the notion of groupoid solved my expository problem, since the Van Kampen theorem extended neatly to the fundamental groupoid, and so yielded an elegant determination of the fundamental group of the circle. Indeed, one obtained a simpler proof of a more powerful theorem, which, as one might say, can't be all bad. Later, in 1967, a famous analyst, George W Mackey, told me how he had been using groupoids for years in ergodic theory. All this convinced me that the thrust of my book should be on groupoids, and that this area of basic theory was most naturally expressed using that term and that language. This became the pattern of the book, published in 1968, and now revised and republished as Topology and Groupoids, 2006.
The excitement of this extension from groups to groupoids was based on the very wide and important uses of groups in mathematics and science, particularly in applications of symmetry. The obvious question raised by this was to what extent parts of mathematics and science which used groups could be better served by using groupoids.
I was brought up in homotopy theory, which studies higher dimensional versions of the fundamental group, called higher homotopy groups, basically by replacing what might be thought of as loops of strings, by their higher dimensional versions, the n-spheres, which for n = 2 are just the surfaces of balls. Could there be higher homotopy groupoids and a higher dimensional version of the Van Kampen Theorem? By now I was very familiar with the proof of this theorem, since I had written it out say five times in various versions. It seemed quite clear that if one had the right language of higher homotopy groupoids, then the proof of the Van Kampen theorem would generalise, at least to dimension two rather than one, and probably even further. So I had an outline proof in search of a theorem. Unfortunately, the theorem itself could not be formulated because the statement required several concepts which had not been defined, and which indeed were unclear.
This started me out on a long road. Every so often I would say ``Tonight's the night!", and start to write the basic paper in the area, giving the basic definitions and propositions, only to find it drifting into the sands, and getting thoroughly stuck. The questions, though, always seemed to recur, and the drawing of a few diagrams kept on strengthening the conviction that they must represent some real mathematics. There was a bit of the old adage: ``If a fool will but persist in his folly, he will become wise!"
Gradually, with clues and methods from here and there, through collaborations with Chris Spencer in 1971 and 1972, with Philip Higgins for twenty years from 1974, with Jean-Louis Loday in 1981 to 1987, with research students who inputted key ideas and results, and contributions from others, a large theory and method took shape. It really is true that a higher dimensional group(oid) theory exists, which is not available for groups alone, and that a number of phenomena in topology, and even in group theory itself, can be better understood, and new results found and proved, from this viewpoint. The higher dimensional Van Kampen theorems also express, and have their roots in, some long standing traditions in topology and group theory, such as the notion of a "cycle", namely ``something'' with no boundary, like the surface of a sphere, and also with methods of gluing, or "adding", pieces together to make larger pieces. I have used these vague words deliberately, since the early literature is unclear as to what is a cycle, and how one ``adds" pieces. The later clarifications, in terms of chains and homology, use a trick of working with formal sums which has a considerable success, but does not fully represent the intuitive idea. The intuitive idea is that of gluing bits a and b together, rather than writing a ``formal sum" a + b. Finding some mathematics which represents this idea ends up by yielding a statement and proof of the above theorem, and so allowing for new understanding and new calculations in homotopy theory not currently possible by other methods. These calculations are not the main aim of the theory, but they are satisfactory as a test that the ideas are working, and that they do something new.
Chris Spencer remarked that a strange feature of work in this area is that you can get very confused, until suddenly you realise that you have not been doing the ``natural" thing. When you do so, it all works out beautifully. This gives a comforting feel about the area. On the other hand, the theory in dimensions greater than 2 was much more technical to find and write down than I had naively expected, and it would not have been done without the high level and varied knowledge and skills of those who came to work in the area.
This theory has not solved any really famous problem. Rather, it has solved problems not previously formulated, and suggested a new set of problems, and areas of investigation. Also, there is a strong intuitive pull. Draw a square, then divide it into smaller squares, and you can easily convince yourself that there has to be a theory which expresses the way the big square is built up. The algebra which expresses this should be of general importance, since the method of building a complicated object from small standard pieces is quite widespread. It is interesting to see the conceptual and technical advances that are required to express these ideas, even in the simple format used so far.
History shows that, in the long run, new methods win out over new theorems, and over the solution of famous problems. The latter can often be more in the nature of a test of a new method rather than an indication of what the method will eventually achieve.
The aim of the theory of higher dimensional group(oid)s is that it should come to bear to ordinary group theory a similar relation to that of many variable to one variable calculus. This may seem a case of overweening ambition. On the other hand, it is difficult to resist the voice which whispers: ``It is ambitious, but what if....? How do you know it can't be true? Which of the prospects, true or false, would be most fun? What needs to be done to make it work?" [This page has had over 13,000 visits since May, 2000, which is some measure of interest.]
It is by this stage, after almost thirty years of thinking, off and on, about this area, difficult for me to see what might be the obstruction to this happening. It will be interesting to see what actually happens.
These experiences have led me to emphasise the conceptual mode of progress in mathematics. This allows for the view that good mathematics can be easy. On the other hand, it should also be said that the technical requirements to set up these concepts in this area, and make sure they work, are considerable, and not what I had expected to happen. One aim of mathematics is to set up machinery of which you do not need to know or test all the parts before you use it, just as you can drive a car without knowing the workings of the internal combustion engine. This is the function of lemmas and theorems.
These points are relevant to a recent debate, sparked off by an October, 1993, Scientific American article on ``The death of proof". A point that I think has not so far been made in this debate is that mathematics increases certainty by the development of new concepts, and the formalisation of ways of thinking, so that the framework of an assertion and its proof can become so well structured, so natural, and each part so well tried, that the whole carries conviction. What one calls a "good proof" is not so much like finding a route through a maze, with possible errors at each stage, but like following a walk through a natural seeming landscape, to a suprising viewpoint.
Postgraduate education represents perhaps an extreme of individual involvement in mathematics training. I have had the privilege of taking twenty one people through to a successful doctorate degree. From all these students I have learned a lot, since their problems and approaches to mathematics have all differed considerably. But this number does contrast with the hundreds of undergraduates whom I have taught over the years.
I still find training postgraduates to work for a doctorate a risky business. My overall method has been to involve students in the problems in which I happen to be interested at the time, and to discuss frankly how one would reasonably assess progress in this particular field. In this process, some students have made quite crucial contributions to the overall research programmes, in ways which I would not have foreseen and quite possibly would not have worked out for myself.
I think that in all cases, work has been done which otherwise would not have been done. It was partly forced by the necessity, particularly from the student's point of view, of some kind of progress, and so for an analysis of how we should proceed. If you have a lot of available questions, and there is no real lack of them in this area, then each one has a lesser priority than the whole programme, and can perhaps be replaced by another. Some kind of ranking, of value judgement, is crucial for the researcher in deciding what to tackle next. For the student, though, the most important problem in the world is the one that he or she is tackling, and there is a special urgency about getting somewhere.
The process of training and discussion, of making students aware of available strategies of work and study, is of course individually intensive, involving in some cases many hours of discussion and of reading student's work. In some cases, the opposite has taken place, and I have been instructed how the problem should be tackled! What I have provided then (I hope!) is the context and the problem, with the reason for wanting this problem solved.
All the problems given to students have tended to be my problems, that is the problems thrown up in studying this area. This has the possible danger then of leading students into a byway of mathematical progress. Fortunately, these sets of ideas have come more and more to link with, to require and to illuminate known areas. This fact was comforting in judging the progress and prospects for the overall area.
In fact critics of papers and grant proposals have suggested that this area is `irrelevant to mainstream algebraic topology'. This shows the social difficulty of attempting to change basic paradigms. Also the `mainstream' of areas are well known to flap around like the sails on a yacht (to mix a metaphor). The aim of this theory is to dig a new channel from the intuitive sources of algebraic topology to allow the growth of a new area of development.
A severe problem in postgraduate training is that of background. A certain knowledge is necessary to understand the problem and its context. An even greater background is necessary to understand and master the tools which should be relevant for the study of the problem. Many of these tools are learned ``on the job", and, there is a judgement required as to a ``need to know". There is no easy answer to this. Most problems require for their solution a degree of skill in certain specific areas, from say group theory to programming in C, and without these skills at a professional level no worthy progress will be made. How much do you need to know to undertake mathematical research? The famous answer is: "Everything, or nothing!" (Quoted in E.T.Bell's `Men of mathematics'.)
There are two main procedures which have over the years evolved as important for postgraduate training.
The benefits of the process of writing mathematics
The main idea is that writing mathematics to a high standard of exposition is a crucial element of doing mathematics. It took a long time for me to realise for myself that this was crucial in my own mathematical work. As explained earlier, the writing of a book on topology set a course of many years of research work.
So our postgraduate students are set as part of their work the task of writing up a piece of mathematics, not just by copying from a text or from various papers, but to give an exposition of one area from a different viewpoint.
The growth in the use of mathematical wordprocessors has been a great help in this process. The tutorial process of instruction can work on a readable typed text, which can be improved, and the process of making mathematics is seen as the production of a finished, accurate, clear and readable work. This allows for an emphasis on the craft of mathematics, and so on its nature as a process. The art comes in the analysis of the qualities in the finished product for which one is looking, and the decisions on how to achieve them. It is very helpful to students to have these matters discussed.
The analysis of aims
The idea here is to explain to a student what it is that might be done, and then to discuss the following:
Why have I, the professor, not done it before? Answers might be:
How should the answer or answers to the previous questions be used to influence the immediate tactics?
For example, it might be necessary to do a serious study of a particular part of the literature, to learn some skills from a given area, or to evaluate new evidence that the problem might be more important than previously thought.
What would be the expected results of achievement of the immediate aims?
Some judgement as to the value of the proposed achievement must be made, if a student is to spend some time on it. If students are given the impression that they are asked to pick up `crumbs from the table' (an expression I have heard used by senior mathematicians), who can be surprised if they take up other activities? As Tom Watson of DNA fame wrote: `Big questions get big answers.' What might be a `big question' in mathematics? Is it only a famous conjecture, or could it also be the opening of window onto a possible new landscape? Can precisely formulated conjectures come under the term `big questions'? There is a troublesome belief around that `big questions' are to be asked only by `big people' in departments of an appropriate `critical mass'. Our doctoral students have enjoyed asking fundamental questions!
There needs to be a ``fall forward" position: what do we do if the problem is far easier than had been thought? Where do we go on?
There ALSO needs to be ``fall back" position: what do we do if the problem as stated is far harder than anticipated, or, even worse, not as sensible as originally thought?
Is the advice of the supervisor sensible?
It is often hard for students to realise that while it may be the job of the supervisor to have ideas, and to suggest ways forward, it is for the student to evaluate them.
It is useful to work on the following analysis. If 3% of your ideas are good, and you have 100 ideas, then you have 3 good ones: result, happiness. If 3% of your ideas are good, and you have 10 ideas, then you have problems: result, misery.
For this reason, it is useful to see how the supervisor copes with failure. Indeed, a part of the success in research has to be the successful management of failure.
Is the problem a natural one for the student?
Jose Montesinos said that his advice to students was to continue with those aspects they found easy! It is difficult to describe exactly what it means to understand mathematics, and even von Neumann commented: ``You don't understand mathematics, laddy, you just do it!" Each person's mental equipment, and natural mode of thought, differs from those of others, by reason of both genetics and of experience. Only trial and observation can find which problems are the most appropriate.
Skill learning
Of course, if new skills have to be learned to carry out the work, then the usual methodology of skill learning applies, namely:
The motivation for the skill learning is important, and that is why I have put task analysis at the beginning. A severe problem of mathematical teaching is to give motivation for the skills which are learnt. Many have given up on aspects of mathematics as they could not see the point. I have seen as external examiner for undergraduate degrees many courses for which the motivation for the topics chosen was unclear.
Conclusion
The output of postgraduate education is, in theory, a trained independent worker, with a proven battery of skills and knowledge, and with some idea of how to make judgements in seeking out and inventing problems, reading and evaluating the literature, making progress with problems, writing up the results, and evaluating the results achieved, and able to communicate them to others.
The problems my students have been asked to tackle have sometimes turned out remarkably hard, so that the discussion of what might be partial progress has been important. One student said that a good aspect of this programme has been the combination of grand prospect, strong intuitive base, and the technical problems that needed to be overcome to make this intuition work. Also, I cared strongly about the results, and was delighted that on many occasions I was shown how to do things.
The supervisor has a great advantage over the research student in the knowledge of background, context and notion of value. On the other hand, each student is an individual, and each is likely to respond differently to different kinds of mathematics.
I do not think there is any final answer to the methodology of postgraduate education. As with many activities, it is possible to point to some avoidable mistakes, such as that of assuming something is ``obvious" without writing down all the details, and also to give some kind of framework to the doctoral process. Part of the problem seems to be to combine a sense of direction, with the ability to take note of promising lines if and when they appear. A considerable part of the difficulty is to acquire the necessary background and skills to understand, evaluate and tackle the problems. Since a lifetime can be spent in acquiring knowledge which might be useful, a pragmatic attitude has to be taken of learning what seems to be necessary to get on with the job.
On the other hand, when a skill is necessary, then it has to be learned. You cannot make an analogy with, or use a method from, an area of which you know nothing.
There is no advantage in reinventing the wheel, except as a learning method. The spirit of Polya's ``How to solve it" is relevant, but we need a further trick, against the spirit of his book, namely ``Look it up in the literature". A student would feel aggrieved if he had been slogging away for six months at a problem the experts know has been already solved, or would fall easily to a range of standard techniques. So there has to be a search for those methods which are in the literature and which might be relevant. We are not playing a party game, and doing research is difficult enough without artificial restrictions. A paper reproving something already known will get short shrift from a referee, unless a new viewpoint or simplification is apparent.
The acquiring of necessary skills is no easy task. The teacher and the student have to allow for time, practice, repetition, and thought. Persistence is important, since it may take a long time of apparent no progress before it is apparent that real improvement takes place.
There is also the question of what level of skill is required for the problem at hand. I like the comment of a magician who explained:
I practice till the difficult becomes easy; the easy becomes habit; and the habit becomes beautiful.
Even if practice does not necessarily make perfect, it is clear that practice is an essential element of perfection. There is no way to become a good swimmer, a good musician, without putting in the hours to get the feel of the activity, on the basis of sensible coaching and teaching. But how good do we need to be for the purposes at hand? What do we have time for?
Is there a danger that the baby of practice has been thrown out with the bath water of rote learning? You tend to get funny looks at educational conferences when you bring up the topic of rote learning, but have the psychologists analysed for us the differences between rote learning and practice? I have met education students who have learned by rote that rote learning is a bad thing! Has anyone shown us a royal road to mathematics? It may be that if we ourselves cannot understand the processes involved in carrying out an activity, then we are left the notion of practice until we get the feel of it ourselves. How many activities can we really understand in a way which helps with the teaching of them? This is the advantage of concentrating on the notion of output, and its quality.
I have been involved in mathematical popularisation. I have given three addresses to the British Association for the Advancement of Science (1983, 1987, 1992), in the last case as President of the Mathematics section. I have given a London Mathematical Society Popular Lecture (1984), a Mermaid Molecule Discussion (1985), and a Royal Institution Friday Evening Discourse (1992). This last was particularly exciting and taxing, since it involved not only a lecture but also a library exhibition. I have also been involved for ten years in the Royal Institution Mathematics Masterclasses for Young People in North West Wales, where we take about fifty five school children aged thirteen for five Saturdays fortnightly. A team at Bangor spent four years preparing an exhibition Mathematics and Knots, for the Royal Society PopMaths Roadshow, which circulated the UK in 1989 and 1990, starting at the ICMI89 meeting at Leeds on "The Popularisation of Mathematics".
Problems of the popularisation of mathematics
The overall aim in these lectures and exhibitions was to convey to a broad audience something of the methodology and nature of mathematics Part of the problem is thus to make abstract ideas concrete, to give advanced mathematics from an elementary viewpoint.
Among all the subject areas, mathematics has a special difficulty in popularisation since the general public have little ideas on what are even some of the most basic objects in mathematics, such as that of a group. Part of the theme of this article is that this lack of knowledge is in part traceable to a lack of clarity in the mathematical community, by both researchers and teachers, as to the nature of mathematics itself, and so to a lack of clarity about conveying this to the general public.
The nature of mathematics
My popular lectures aimed to convey some aspects of mathematics related to each other. These aspects were exemplified with two demonstrations in the Washington talk, which it is worth explaining here, and which were necessary to give on that occasion, since I had brought the things 2000 miles!
Mathematicisation
One of these was the aim in mathematics of mathematicisation, that is of expressing an intuitive idea in a format which is sufficiently precise to enable deduction, calculation and proof. There is usually a prior stage to this, that of conceptualisation, which also requires its own analysis.
Rules and laws
Mathematicisation usually involves the notion of a rule or law. One example of this which I used in the lectures was in the theory of groups, and the calculation with relations on symmetry operations.
The mathematicisation of symmetry can be demonstrated through the particular example of the symmetries of a square, which can easily be done for a large audience with a large cut out square with labelled corners. It is easy to show the rules where x denotes rotation of the square through 90o, clockwise, say, y denotes reflection in a bisector of two edges, 1 means the operation which leaves the square alone, and xyxy means do first x, then y, then x, then y. The point here is that the representation of an action by symbols, of consecutive actions by concatenation of symbols, and the use of the symbolic method generally, is one of the greatest difficulties the general public find in getting a glimpse of what mathematics does. So it is necessary to show this feature in a concrete situation, and then to go further and show the value of the symbolic representation through the use of rules on combinations of these symbols for explicit calculation, and to show how this calculation models real operations.
Another nice feature of this example is the importance of pedantry, in this case the importance of taking note of the operation 1 of leaving the square alone. Without this, the rules for the symmetry could not be properly expressed, just as our counting system would not work without the use of the number zero.
There is a nice trap here about this representation, which shows the importance of precision. When you rotate the square, the labels on the corners change their position. But one wants to iterate the operation x. So x has to be an operation which works on positions, that is it moves all the elements in their various positions one place around clockwise.
One has also to be careful, because the notion of clockwise differs between the audience and the demonstrator. This gives an opportunity for another remark on symmetry.
Idealisation
This is a standard procedure. The real square is not completely symmetrical. For the mathematicisation, we think instead of an ideal square.
Abstraction
This symmetry example also shows the importance of abstraction, namely representing the real operation of rotation on an ideal square by a symbol, and representing the combinations of operations by combinations of symbols.
This abstraction is usually a stumbling block for the general public. However it is crucial to the progress of the subject since it allows the notion of analogy, an aspect of mathematics not commonly stressed.
For example, when we write x+y = y+x, and xy = yx, we are illustrating the commutative law and so illustrating an analogy between addition and multiplication. This process of analysing and using laws at various levels in the subject is very important. For example, algebraic structures are an important part of mathematics, but there is also a mathematics of algebraic structures, in which such systems are looked at as a whole. Thus analogies work between levels of abstractions as well as at one given level. The symbolic method is a crucial part of the process of abstraction, since symbols can represent a variety of things.
Deduction and calculation
A further part of mathematics is the deduction from and calculation with rules. In the case of the symmetries of a square, we want to deduce from the rules given above that, for example, xy = yx3, yx = x3y. This shows that whenever x is taken past y it changes to x3. The carrying out of these kinds of deductions and calculations is an important part of mathematics.
The learning of algorithms
In some circles of mathematicians, the ability to learn and carry out algorithms is rather decried. To the contrary, I believe it is a basic part of mathematical skills, just as hitting a ball consistently is a basic part of tennis. Mathematics involves of course far more, namely the ability to solve problems and develop theories by the planned use of basic algorithms and methods, and also by the effort to see their scope and limitations.
Surprise
Some of the best mathematics has about it the element of surprise, the revealing of a fact one would not have thought possible. Such a surprise makes one want to explain why this happens. Here is an example.
Dirac String Trick
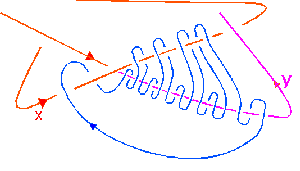
The Dirac string trick illustrates a surprising feature of space, and also the notion of a rule or law. The apparatus for this is as follows.
Take two squares of card or board, say 18" square (0.5m), and on one you draw an arrow, to indicate direction, or place a picture. The corners of the top square are then connected to those of the bottom square by string, or, better still, different coloured ribbon.

Figure 1
It is a good idea to clip the ribbon to the board by bulldog clips, so that the apparatus can be untangled easily.
Hold the bottom square on the floor by your foot, and rotate the top square through 360o, keeping it horizontal. The ribbons become tangled.
Now rotate the top square in the same direction through another 360o. It appears that the ribbons become more tangled. However, it is possible to untangle them completely, moving the top square up and down to allow room for the ribbons to be manipulated, but without altering the direction of the top or of the bottom square.
This illustrates the law x2 = 1, where x is now the rotation of the square through 360o.
There is a more subtle point which accords well with my research interests. The proof that the rule holds is obtained by untangling the ribbons. However, the finding of such an untangling, and the classification of these untanglings, is a ``higher dimensional problem", of a much greater difficulty.
It is amusing to try variations on the above, such as rotating the square about a different axis than a vertical one.
Dirac's interest in this trick was the argument that it was a model of the spin of an electron. This analogy is quite a good one, once the exact mathematics of the situations has been spelled out.
For more information, see some pages on the Projective Plane.
[Note added October, 2006: The mathematical paper relevant to this trick is Newman, M. H. A. On a string problem of Dirac. J. London Math. Soc. 17, (1942). 173--177, which shows that the strings cannot be untied after one twisting. It has been proved that the quaternion group can be modelled in this trick. ]
Knot theory
Here is another ``trick" which also illustrates some mathematical methodology.
Make out of copper tubing a pentoil knot as shown in thick lines in
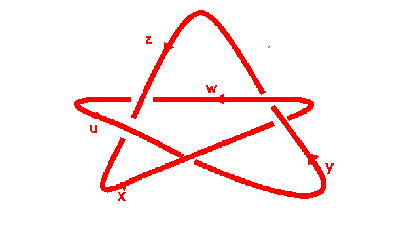
Figure 2.
(This needs professional help, such as an engineering workshop, to make it look good, but you can make it yourself with thick wire.) Now tie string on according to the following rule:
xyxyxy-1x-1y-1x-1y-1
as shown in the picture, and tie the ends of the string together. It is then possible to take the loop of string off the knot without cutting or untying it. That is, the above complicated formula also in this situation represents, or equals, 1. It is even possible to give the proof of the formula for bright youngsters familiar with some algebra, such as cancellation.
One of the reasons for the choice of knot theory for public lectures is that it illustrates a number of mathematical principles, and yet the basic problems can be put over in a direct fashion by using a piece of rope. You could also look at our web knot exhibition. , and the article `Making a mathematical exhibition'.
Conclusion
There is no space or time here to discuss the wide topics of output at undergraduate and at school level. Each of these represents a very big problem. It is an important fact about the undergraduate output that our teachers of mathematics, at least in the UK, largely come from this group of undergraduates, so that attitudes fostered at Universities have a large influence. There is even a question as to whether in fact any attitudes are deliberately fostered.
Here is the elephant analogy: We can teach the structure of the elephant's trunk, tusks, skin, feet, stomach, and so on. But can the elephant really be understood without a global approach, an ecological and evolutionary approach?
There is a worry that students of mathematics are starved of any attempt at a global viewpoint, and a sense of value and of context, an understanding of the place of mathematics as a human endeavour. If prospective teachers do not get such a viewpoint at University, and the language to express it, what can they communicate to their pupils? How much of the problems of recruitment of mathematics undergraduates are due to this factor?
I am sure that those who came to ICMI94 are aware of these concerns, and that the work of ICMI will help to develop not only teaching in mathematics but also a general awareness of these issues.