By Ronnie Brown, Professor Emeritus, University of Wales Bangor.

Abstract:

Contents.

I. Introduction

Mathematics is an unseen, and usually unsung, part of our daily lives. It lies behind: econometric models; body scanners; aeroplane design; medical statistics; CD players; engineering; the theory which enabled the error correction to reconstruct stunning pictures from the Voyager II mission; the design of computers; and a host of others. Consider also the graphs we see in our daily papers: inflation against time; sales against time; risk of cancer against number of cigarettes per day. This concept of a graph derives from the application of algebra to geometry, through the Cartesian coordinates invented in the 17th century. So mathematics is involved in matters of life and death, profit and loss, work and play. Parts of the language of mathematics, for example, number and graph, devolved over the centuries into everyday life.

Mathematics also leads science. The great physicist, Paul Dirac, in one of his last addresses, explained his own credo (quoted in [12] p.63):

"One should allow oneself to be led in the direction which the mathematics suggests... one must follow up a mathematical idea and see what its consequences are, even though one gets led to a domain which is completely foreign to what one started with.... Mathematics can lead us in a direction we would not take if we only followed up physical ideas by themselves."

For mathematics to lead in this way, it has to exist. It is not generally recognised what an extraordinary range of new mathematics is being found. The aim of this discourse is to describe just one example of new mathematics, which I and others like to call Higher Dimensional Algebra. It is a pleasure to convey something of the story of what seems likely to be a new discipline in mathematics, and one which opens out a new world of concepts and applications.

I will explain also the background to this approach, not exactly with the original ideas, which are almost lost in the murk of history, but in a more concrete and explicit form, and so give some impression of how concepts can be brought out of the dark.

Let me stake my claim that mathematics is about ideas, concepts, and visions. The craft is how to make these real and rigorous.

II. Formulae in a Line or in a Plane

Here is an illustration of our idea of higher dimensional algebra. Consider a simple and well known formula,

(x - y)(x + y) = x² - y²

but now with each symbol written on a children's block, as in Fig 1:

If the formula is not familiar, that does not matter. Everyone knows mathematics is concerned with x 's and y 's and that formulae of this kind occur. But note one of the characteristics of this formula: each symbol in the formula is related to those to the left and those to the right, according to standard rules. Further, this arrangement corresponds to our standard mode of writing.

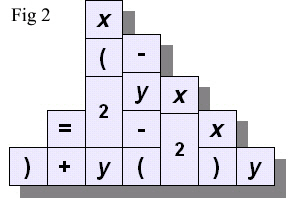A temptation with a row of children's blocks is to build them into a wall, as in Fig. 2. This unfortunately turns the formula into nonsense. It would be even worse if we built a tower!

However, this very temptation leads to some naive questions (and we know from history that the best science starts from simpleminded questions):

Is there some mathematics which corresponds to this new arrangement? Is the convention of mathematics on a line a necessity, or a question of habit? Suppose there were a mathematics, an algebra, in which symbols were related not only on a line, but also out of line, in a plane, up and down, or even out of the plane. What would this mathematics be like, and what would it do for us?

I shall immediately give an illustration of how thinking "out of line" ie in more dimensions, can be illuminating and suggestive. Consider the formula and the graphical representation in fig 3.

The arithmetical formula is correctly formed and perfectly straightforward to anyone with a knowledge of the arithmetical symbols and "in a line" structure. But without this mathematical language knowledge? The pictorial representation in 2 dimensions however can be regarded as self explanatory! In mathematics we want the notation to have a structure that aids intuition and calculation, to make things easier. Historically this kind of advance was obtained, for example, in moving from Latin (I, II, III IV etc) to Arabic numerals.

This questioning of our standard notation is the main background to this Address.

I would also like to give the authority of Einstein (1916) for the questioning of standard usage:

"For when I turn to science not for some superficial reason .... then the following questions must burningly interest me as a disciple of science: What goal will be reached by the science to which I am dedicating myself? To what extent are its general results `true'? What is essential and what is based only on the accidents of development?...[my italics] ...It is therefore not just an idle game to exercise our ability to analyse familiar concepts, and to demonstrate the conditions on which their justification and usefulness depend, and the way in which these developed, little by little..."

The question on the rearrangement of the blocks is actually more complicated than necessary, since the formula given includes addition, brackets, multiplication, and equals. Here is a simpler question. It is standard practice in mathematics to express a diagram of labelled arrows as in Fig. 3

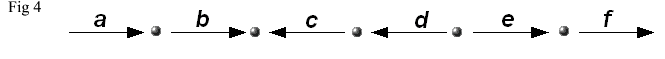
by the formula

abc^-1d^-1ef

where a reversed arrow is represented by the inverse, i.e. by c^-1 instead of c. This presents no problem at all, and is very familiar. Now consider the following diagrams :

What is embarrassing is that, while the one-dimensional answers are simple and straightforward, with formulae on a line of a standard type, yet it is not apparent where to start to write down anything which makes sense in answer to the question in just one higher dimension.

These questions occurred to me in 1966. I had an idea that there was a mathematics in which this 2-dimensional algebra made sense, and which would yield a formulation and proof of a new and potentially important version of some basic ideas in topology, centred round how to model the building up of big spaces from their parts. This application (what are called the Van Kampen Theorems) is still for me the core of the future of higher dimensional algebra. But note the interesting point of methodology: I was not trying to solve a specific problem, of the form "Is statement A true or false?", but instead proposing to produce a new type of mathematics, with certain characteristics, and which, if realised, should allow for the solution of problems, without, at that early stage, specifying which problems.

The process here is that of devising a new language to express and realise intuitions. It involves the formulation of new concepts, and this leads to new problems. This is one of the major forms of progress in Mathematics, allowing the opening up of new arenas.

The mathematician regarded as the the 20^th century master of the development of new concepts referred, in correspondence to this author, to

"the difficulty of bringing new concepts out of the dark"; (A. Grothiendick pers comm.).

How new concepts and ideas can change things is entirely topical of course in this era of the internet and rapid technological development. A good example from mathematics is the concept of zero, which we understand became accepted (in western Europe) as part of the renaissance and is a foundation stone of all subsequent arithmetical calculation. Indeed what mathematics does is develop language for expression, description, verification and calculation.

It was a surprise that just to make initial progress in higher dimensional algebra was not easy, but the intuitions were so strong the ideas would not go away. The programme turned into a major undertaking, to date involving, with me alone, eleven co-authors from seven countries (Hong Kong, UK, Germany, France, Poland, Ireland, USA), and ten research students at Bangor and Durham (who made crucial contributions to the theory). The first paper was published in 1976, ten years after the start. By now there is a rich and tightly knit theory which encapsulates the original intuitions, performs the job that was intended, allows for new calculations, and opens out many possibilities for the future.

The first question was where to start. The aim was this potential Generalised Van Kampen Theorem. In its standard form in dimension 1, this theorem used the notion of abstract group, and I had shown in 1965 that the standard theorem could be improved by using the less usual notion of groupoid instead of group. It seemed reasonable, even necessary, to ask to what extent groupoids, rather than groups, could be used in the higher dimensional theory. It seemed no one else had asked this question, partly because groupoids were generally not well regarded as a tool in mathematics.

To show why these questions had prospects of being important, I will explain the relevance of the terms group and groupoid to three great themes in mathematics: Symmetry, Space and Motion. I will also use these themes to describe the main features of the search for the unknown forms of higher dimensional algebra.

III. Symmetry and Abstract Groups

The mathematical structure expressing the notion of symmetry is that of abstract group. To explain this, we examine the nature of symmetry.

The importance of symmetry

Here is what the great mathematician, Hermann Weyl, wrote on symmetry:

"Symmetry establishes a ridiculous and wonderful cousinship between objects, phenomena and theories outwardly unrelated: terrestrial magnetism, woman's veils, polarized light, natural selection, the theory of groups, invariants and transformations, the work habits of bees in the hive, the structure of space, vase designs, quantum physics, scarabs, flower petals, X-ray interference patterns, cell division in sea urchins, equilibrium positions of crystals, Romanesque cathedrals, snowflakes, music, the theory of relativity." [17]

That is quite a list - and only a sample!

To see how mathematics comes in, and allows calculations, let us take a simple example:

 We represent the symmetry of the square by considering all the eight movements which take the square to itself. This consideration of all movements, this global viewpoint, is a common feature of mathematical practice. Among all these movements, we consider two basic ones from which all the other symmetries of the square can be built:

x =: Rotation anticlockwise through 90°
y =: Reflection in a vertical line

So x is represented as in Fig. 8 and y is represented as in Fig. 9

Here x and y move whatever is in the positions at the corners into new positions. Given a symmetry operation, we can do one after the other. If we do x , the rotation through 90° , four times, we get back to where we started (Fig. 10)

Fig 10

If we do y twice, we also get back to where we started. These facts are expressed symbolically by:

Notice that we use the symbol 1 to denote the operation of leaving the square alone, of doing nothing. These rules are called relations on x and on y.

A third rule or relation is more surprising, and cumbersome to express in words: It can be shown as in Fig 11:

It is now the technical job of a mathematician to work within these rules, and to make deductions. For example, we can find that

These last two rules can be summarised as: x changes to x³ when it moves past y.

This fact, and the rules x⁴ = 1, y² = 1, are all that is necessary to allow for calculations in this group of symmetry operations of a square. The rule xy = yx³ is surprising, since multiplication of ordinary numbers satisfies the rule : xy = yx . This rule is called the COMMUTATIVE law.

That it does not hold for symmetries in general is crucial for the theory of symmetry, and will recur when we come to discuss the higher dimensional theory.

The eight symmetry operations of a square, with their 64 products, form an example of a symmetry group. This symmetry group is a special case of the general notion of abstract group.

Abstract group and structure.

Here we come to a key notion we have to explain, the notion of an abstract structure. It is a very difficult notion, but it is at the heart of the nature of mathematics. These structures are among the objects of mathematics in the same way as animals are the subject of zoology, molecules of chemistry, and so on. What then are structures?

Mathematical structures are used to describe not things themselves, but relations between things, or how parts of objects are related. This involvement with relations between things is why mathematics is an abstraction from the real world. This also is its power, since the patterns of relations we perceive and abstract can often be found to occur in a variety of places and situations, and this leads to analogies and transfers of information.

A mathematical structure can be thought of as like a game, consisting of pieces, modes of combination, and rules (although a precise definition requires quite sophisticated mathematical language). Once you accept a game, then you work out the consequences of the rules, and see what the game is like, and what will happen as the players pursue various actions. A similar procedure applies to mathematical structures.

This working out of the consequences of the rules is not a mechanical procedure. E Wigner writes in his famous essay "The unreasonable effectiveness of mathematics in the physical sciences": "I would say that mathematics is the science of skillful operations with concepts and rules invented just for this purpose [i.e. of skillful operation with concepts and rules!]. ...the principal emphasis is on the invention of concepts."

Wigner also emphasises the need to define concepts beyond those contained in the axioms, the basic rules, and "with a view to permitting ingenious logical operations which appeal to our aesthetic sense both as operations and also in their results of great generality and simplicity". [16]

Now I come to the particular mathematical structure of an abstract group. You notice that I considered all the eight symmetry operations of a square, and then considered doing first one and then another. It is this combination (also called product, or composition) that is crucial and for which we try to lay down laws or rules, and so form a mathematical structure. The laws for this structure have to be sufficiently general to be of wider implication than just the one example with which we are dealing, but also sufficiently special to include it.

It is no simple matter to formulate useful mathematical structures. They tend to evolve over years, decades, or centuries, as mathematicians find the rules and combinations that are commonly used, and see what is the pattern that keeps on recurring, and must be given for convenience a special name and habitation.

For our concept of an abstract group, we start with a collection of things, which might be anything, from numbers, to movements of a square or of a triangle, but there has also to be given a method of combining any two of our things, say x and y , to get a third, written say xy . We have to consider both the things and their method of combination together, and we have to suppose satisfied three laws, which are called the axioms for an abstract group.

Axioms of an Abstract Group.

1. There is an identity , usually written 1, so that for any x we have 1 × x = x × 1 = x.
2. Any x has an inverse x ^-1 for which xx ^-1 = x ^-1x = 1.
3. Associativity , which essentially states that there is only one way of multiplying three elements one after the other, in a specific sequence. For those familiar with symbols, this says that
   x (yz) = (xy )z (for numbers and multiplication, for example, with x = 3, y = 5, z = 7, this associative rule reads 3 × 35 = 15 × 7).

This notion of abstract group, as above, has been found over the last 200 years to be one of the of the central concepts of mathematics. The formulation of this concept involved the work of many mathematicians and scientists, from ancient Greece, through to the middle of the nineteenth century.

The apparent simplicity of the axioms for an abstract group disguises their power. Groups are used in chemistry, crystallography, the physics of fundamental particles, the design of wave guides, dynamical systems, in fact wherever there is a notion of symmetry, or of some kind of repeated, reversible motion.

Note that in the axioms for a group, we single out the properties of the identity element, namely the symmetry which leaves things alone. Without this "trivial" identity element of symmetry, we cannot formulate the notion of group! This illustrates a feature of mathematics: the importance of pedantry, or of noticing everything that happens, or attention to detail. I have already referred to the importance of `zero' in the introduction. Zero was used in India in the 2nd century BC, and made its way to Europe in the 15th century AD, as a part of the Arabic system of numerals. This system led to the invention of double entry book-keeping, and so, it is believed, to the prosperity of Venice. All this arises from counting the number of objects in an empty box, an apparently foolish undertaking! We will see more of identity operations later.

The symmetry group of the square has 8 elements. It is a fairly simple structure. The symmetry group of a cube has 48 elements. There is an enormous variety of groups. The classification of finite groups, and particularly what are called, possibly misleadingly, simple groups, has been an astonishing undertaking, involving many mathematicians, and the final proof of the classification of finite simple groups occupies some 15,000 journal pages. So a few simple rules can define complex structures, whose analysis and description may require a lifetime of study. This so far does not give us any clues as to what might be a "higher dimensional group". For this, I have to show another way in which abstract groups came on the scene, through the study of space and motion.

IV. Space

In the time of Euclid, geometry was seen as the study of our three dimensional space, and the properties of this space were reduced to some "self evident" postulates and axioms, from which further properties (constructions, propositions and theorems) were deduced.

The mathematical view of "space" has changed radically since then. Now mathematics abounds in structures called a "space" of some kind. The dimensions of these mathematical spaces range from zero to infinity, even to what are called uncountable infinities, and the notion of dimension has been enlarged to include fractal spaces, with fractional dimensions, which are used in the study of chaos. The applications of mathematical space range all over science, from fundamental particle theory, to statistics. A relation with the artist's view of space is shown in the works of the sculptor/mathematician Helaman Ferguson [11], and the sculptor John Robinson [15].

It is necessary to give some impression of the intentions of a mathematical space. I will illustrate this first in relation to the notion of symmetry, by borrowing some results of Stuart Robertson, of Southampton University, who has supplied the design of the models for 22 objects displayed in this Address, which we call Robertson's cuboids. All of these 22 objects have 8 vertices and 12 edges, and their 6 faces are plane quadrilaterals. Some of these cuboids are more symmetrical than others. In order to explain this, it is convenient to move down a dimension and look at squaroids (again, Robertson's term), that is the plane quadrilaterals. Robertson classifies these into symmetry types [14].

TABLE 1

OBJECT	NAME	SYMMETRY	DEFICIENCY
	Square	8	0
	Rectangle	4	1
	Rhombus	4	1
	Parallelogram	2	2
	Isosceles trapezium	2	2
	Deltoid	2	2
	Asymmetric Quadrilateral	1	4

The column "symmetry" gives the number of symmetry operations, including the identity. The column "deficiency" is more important for our purposes.

First, two objects are called "similar" (in the  familiar "Euclidean" sense of having the same geometry) if one can be transformed to the other by reflection, rotation, translation or uniform stretching or contracting in all directions. So all squares are similar, as are all cubes.

Now we have to imagine a "space" of all these symmetry types. In this space, there is only one point for the square, since all squares are similar. So the "deficiency" of the square is the dimension of a point, which is 0. However two rectangles are similar if and only if they have the same ratio of the longest to the shortest side. This ratio, a number greater than or equal to 1, specifies the similarity class of the rectangle completely. The "space" of these types of rectangles can be pictured as a part of a line starting at 1, which represents the square, and going away indefinitely......

Since a line has dimension 1, or "one degree of freedom", the rectangle is said to have deficiency 1. A rhombus is specified up to similarity by an angle between 0° and 90° . So the space of types of rhombuses can be pictured as a part of a line:

where 0° represents a line segment, and 90° represents a square. The type of a parallelogram is specified by the ratio of the longest to the shortest side and by an angle between 0° and 90° . The parallellogram thus has deficiency 2 and its symmetry space looks as in Fig 14:

where the bottom line is omitted since for angle 0° a parallelogram becomes a line segment, of deficiency 0. We leave the reader to picture the symmetry spaces of the other squaroids. The spaces of all these squaroids fit together into one big space of which Fig 13 (rhombuses, rectangles, parallellograms, and squares at the corner) is a part.

Now let us move to three dimensions. The cube has already been pictured. It is one of the five regular Platonic solids whose explanation was one of the aims of Euclid's Elements of Geometry. All the Platonic solids have deficiency zero: for example, any two dodecahedra are similar to each other. By contrast, two rectangular blocks are similar if they have the same ratios of their edges, in order of increasing length. So the symmetry type of the rectangular block is specified by two numbers greater than or equal to 1. Thus the symmetry space of the rectangular block has dimension 2, and the rectangular block has deficiency 2. There is a cuboid with no symmetry at all, and there is a cuboid with only three symmetries. Each of these cuboids has an associated "symmetry space", consisting of all those cuboids of the same symmetry type. The dimensions of these spaces varies. For some of these spaces, not much is known apart from their dimension. The possible dimensions are from 0 to 11, excluding 8, 9, 10. The 22 objects represent all the possible types of symmetry of cuboids.

For us, these cuboids illustrate at once the two concepts of symmetry and of mathematical space, and also illustrate the use in mathematics of the notion of classification.

V. Motion

We have illustrated the idea that the points of a "mathematical space" can represent data. Change of data may be represented by a motion in that space. This is a profound idea that has had a widespread influence on mathematics and mathematical applications over the 20^th century.

The next illustration of the notion of mathematical space presented during the lecture was a video created using computer graphics at IBMUK Scientific Research, Winchester, (programmed by Ramen Sen). Called 'Pivoted Lines and the Möbius Band`, here is an account of the video (figs 15-26).

Pivoted lines and the Möbius Band .

		We start to simplify our picture. We introduce a sphere, centred on our pivot. We need only part of the line to specify all of it, and so we omit the part of the line outside the sphere. The line meets the sphere in two points, which we show as discs.
		These two moving discs contain all the information about the position of the line, and so we can omit the line, leaving the two discs. The two moving discs still record more information than is necessary. We can recover the line from the information contained in half the sphere (since we know the centre of the sphere). So we gradually eat away half of the sphere, leaving a hemisphere and one moving disc.
		As this disc moves across the equator, it appears on the opposite side of the hemisphere. So we represent the moving pivoted line in our usual space by the picture of a point or disc moving on a hemisphere, with the rule that opposite points of the equatorial circle of the hemisphere are to be thought of as glued or sewn together, since the disc jumps from one point of the equator to the opposite. This gluing cannot be done in three dimensions, so instead what we do is just record the information that this gluing is to be done, as shown by the motion of the disc.
		This hemisphere with parts glued together is a complicated space. There is another useful picture of it, which brings in the Möbius Band. (right). Take small semicircular pieces, including parts of the equator, out of opposite sides of the hemisphere.	Fig 27. Möbius Band.
		We glue these pieces together, with a twist, and they form a disc.We gradually deform the remainder so that it becomes more like a strip.
		Now we can glue together those parts of this strip which should have have been glued as part of the hemisphere. So there has to be a twist as we glue, and we get the famous Band. This extraordinary surface has only one side and one edge, and the edge is like a circle. We will say more about the Möbius Band later. The blue dot is our disk.
		We have replaced our original picture of a moving pivoted line in 3-dimensional space by a point (or disc) moving on a space which consists of a Möbius Band and a disc. The edges of the disc and the Möbius Band are circles, and these circular edges are to be thought of as glued together. Again, we cannot do this gluing or sewing in our real three dimensional space, but we illustrate it by showing our moving disc hopping instantaneously from the edge of the Möbius Band to the disc, and back again (a traced track is shown as the blue line).
	This picture of our mathematical space is convenient for representing types of motion of our pivoted line. The disc now leaves a trail, which joins up to form what we call a loop. This loop represents a regular and repetitive motion of the original line. Now we can deform the loop to show different motions.
	Fig 26. The loop expands off the Möbius Band, onto the disc, and finally down to a point. This point corresponds to a stationary line.

The movement of this loop shows how our two parts of the space are joined. It also shows us the advantages of the new picture: the changes of types of motion are more easily represented in our new model than in our original picture. Our new model allows for a global picture of particular motions of the line in 3-dimensional space.

Another important aspect is that the movements of this loop not only describe different motions, but also give us information on the mathematical space which represents the positions of the line. We are interested not only in movements, but in movements of movements, and so on, and this is an intimation of the higher dimensional theory.

The 'Projective Plane' and the Brehm Model.

There is more to be said about the space represented in the video. Mathematicians call it the "projective plane". This term is used because of its relations to the notion of projection in technical drawing, which concerns looking at a model or object from different viewpoints. There is no way of building the projective plane in 3-dimensional space. This is a mathematical fact, a theorem, but a little experiment will convince you that a disc of cloth cannot be sewn onto the edge of a Möbius Band. The way in which an attempt at this process gets tangled up shows that there might be a model with self intersections. The first of these was produced by Boy, a student of Hilbert, at the end of the last century.

Now to form the projective plane, seven more triangles have to be added. Four of them are added on the outside and cause no problems, but three have to be added to intersect each other inside, like three planes meeting at a point. Instructions for making this model are in Brehm's article.

Dirac's string trick

At one point in the sequence on the video, we have a loop which goes twice round the Möbius Band, and then this loop is deformed off the band and over to the disc, and then to a small loop, and finally to a point, which represents a stationary line. This is related to the famous Dirac String Trick. Take a square and tie the four corners to another larger square by loose string as shown in Fig 19 (alternatively, tie the initial square to the four corners of the room).

These geometrical demonstrations are related to the physical fact that an electron has spin ½. A particle with spin is something like a ball attached to its surroundings with string. Its amplitude changes under a 360º (2pi) rotation and is restored on rotation to 720º (4pi) (see for example, [13]).

At this stage we can also see a glimmerings of the higher dimensional problems. The result of the trick can be formalised by the rule x² =1 where x here represents rotation through 360º. However, you will find that to untangle the string, you have to be somewhat systematic, and the required movement of the string is not easy to describe. It is this movement of the string that represents the higher order information, namely the proof of the relation x² = 1. Further, different ways of untangling the string, i.e. different proofs of x² = 1 may themselves be related, or deformed into each other. Such deformations of untangling may be regarded as information of dimension 3. Thus the relation x² = 1 is the immediately visible aspect of a sequence of higher levels of information and explanation. This sequence of levels occurs also in the theory of computation, where one would like measures of simplicity, or equivalence, of computations.

The Double Pendulum

Here is another example of mathematical space as a repository of motion, in this case the motion of a double pendulum.

Now we can turn the situation round. Instead of using mathematical space to study and represent motion, we can use motion, i.e. paths, to study mathematical space, and to see how spaces can differ. As an illustration of the method, I use knot spaces.

Paths and knot spaces

In Fig 37 we picture a pentoil knot and we also show a path around it. To study the space around the knot, we can fly around it. As we do so, it is convenient to carry a piece of string with us, to record how we have travelled. This string will represent a mathematical path in our space around the knot, and if the path returns back to itself, we call it a loop.

This idea of constructing invariants of a space in the form of abstract groups, or other kinds of algebraic structures, is an important tool for studying geometric problems, and a part of the subject of topology (Topology : the study of the geometry of continuous deformations: - aka "rubber sheet" geometry) is to find such invariants, describe their properties, and calculate them for specific examples. There is an important mathematical principle involved at this point. The fact that the string comes off the knot proves that the relation holds. However, if the string has not come off after some amount of trying this does not prove that it will not come off. So to prove that the trefoil formula will not work for the pentoil, and vice versa, needs some real mathematical work. What is needed is the 1-dimensional Van Kampen Theorem referred to earlier! This illustrates that to prove that something cannot be done is often a difficult and sophisticated procedure. A further point is that there are many different ways of taking the string off the knot.

And so we move towards higher dimensions: the classification of these "proofs" that the relation holds is an example of a higher dimensional problem, requiring a new range of methods.

VI Towards higher dimensions

At last I can move into higher dimensions, and explain how we get a notion which is not exactly a higher dimensional group, but does perform the same intended role. The next stage in the history is 1932, when the symmetry groups and the Poincaré group were standard methods, with applications right across mathematics, and also in science. In that year the Czech mathematician, E. Cech submitted a paper on "Higher homotopy groups" (the term homotopy refers to a particular branch of Topology concerning holes in spaces) to the Proceedings of the International Congress of Mathematicians at Zurich. Instead of mapping loops to a space, his idea was to map spheres. One can also map squares, or their higher dimensional analogue. Cech used one of the dimensions to define the group structure, in a similar way to what I showed for loops. However, Alexandroff and Hopf, the kings of Topology of the time, showed, by using one of the extra dimensions, that Cech's groups were always commutative:

Here is the key idea of why this is so. In two dimensional group theory, based on squares rather than paths, one may formulate the product of two squares as given by any of the diagrams in Fig 45. That is, in two dimensions there is more room to move around, and this leads to the commutativity rule. The 2-dimensional theory is thus simpler than the 1-dimensional theory (which seems absurd!).

On this ground, and because it was felt that the groups must be the same as the already known homology groups, Alexandroff and Hopf persuaded Cech to withdraw his paper and only a small paragraph appeared in the Proceedings of the Congress. Three years later, however, a Dutch mathematician, W. Hurewicz, published four Notes explaining the main properties of these higher homotopy groups, but without referring to Cech's paper, so they have come to be known as the Hurewicz homotopy groups. These higher homotopy groups became very important concepts, with many people working on them, despite or even because of the difficulty of calculating them for some standard spaces. Both Alexandroff and Hopf later admitted their mistake over Cech's paper. In the 1960s, when higher homotopy groups, despite their being commutative, had become a fundamental tool in topology and geometry, Hopf told E. Dyer that it showed the error of people regarding themselves as so great they are able to know what shall be the future.

This commutativity of higher homotopy groups put paid to the hope of a reasonable "higher dimensional group theory", appropriate for work in two or more dimensions, and more subtle than ordinary group theory. A range of other methods were developed to deal with higher homotopy groups, and to analyse higher dimensional spaces. But any attempt to model directly the 1-dimensional theory in higher dimensions was regarded as a failure to recognise a standard, and fairly simple, fallacy.

VI Groupoids: a wider structure than groups.

It was fortunate that, through being led into considering the notion of groupoid, a generalisation of abstract group which had been around since 1926, I and colleagues were able to open the door into a new theory. In 1965 I was writing a text on Topology, and was busy explaining the theory of the Poincaré group, and its calculation by the Van Kampen Theorem. I came across a 1964 paper of Philip Higgins using groupoids in group theory. This suggested turning my exposition away from the standard format, and to put the emphasis on the known Poincaré groupoid.

Groups arise from composing loops as we showed earlier. But in making a journey, you do not always return to the starting point. You might want to move from A to B, and then from B to D. In fact you can continue a journey a from A to B with a journey b from C to D if and only if B = C. (Obvious!) So, we make this intuition into a mathematical structure. The name for this new and more flexible analogue of a group is groupoid . Its rules, its axioms, are as for groups, with the difference that the composite or product ab is not always defined.

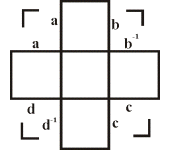
The best way to see this, which emphasises the geometric character of the definition, is to say that for a groupoid we have arrows each with two vertices (fig 46), the source (on the left) and the target (on the right) and that two arrows can be composed to give a product ab if and only if the target of a is the same as the source of b (fig 47).

	Fig 46. Fig 47.

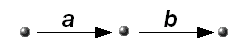One imposes the geometrically obvious notions of associativity, left and right identities, and inverses. Thus a groupoid is often thought of as a group with many identities, and the reason why this is possible is that the product ab is not always defined.

We now know that this apparently anodyne relaxation of the rules has profound consequences. The reason seems to be that the algebraic structure of product is here linked to a geometric structure, namely that of arrows with source and target, and which mathematicians call a directed graph. Thus a groupoid can be thought of as having structure in dimensions 0 (namely the vertices) and 1 (namely the arrows). The linking of these two structures allows for groupoids to be more convenient for modelling geometric phenomena than are groups alone [4]. This came to be the main message of the second half of my 1968 Topology book [5].

We can use this extension from groups to groupoids to study symmetry. Recall that the symmetry group of the square has 8 elements. Now the operation called x rotates through 90° , i.e. takes whatever is in that position and moves it appropriately. Thus the group structure does not fully describe the situation. The full description involves all the eight positions of the square and all the ways of moving between them, a total of 64 elements. These movements, and their compositions, fit together into an abstract groupoid, which gives a fuller description of the symmetry of the square than just the usual group of symmetries. People who work with groupoids recognise that groupoids allow for a fuller and more flexible approach to symmetry than do groups alone.

This notion of groupoid occurs all over the place. In the early part of this century, the mathematician H. Brandt was led to groupoids through his work over many years on generalising work on number theory due to Gauss, one of the great mathematicians of all time. Brandt's paper on groupoids appeared in 1926, and the idea of groupoid was for a long time used occasionally in algebra and topology, not as a necessary or fundamental concept, but with curiosity at the way it sometimes permitted an elegant treatment. This elegance should have been taken as a clear sign that the concept was an appropriate generalisation of groups in many geometrical applications. This recognition is still patchy.

There is now a large literature on groupoids (see [4]), with applications ranging across mathematics, from topology to algebra, and functional analysis. There are applications in physics. Indeed, Connes [10] has recently pointed out that Heisenberg in 1925 realised that the Ritz-Rydberg law for the spectrum of hydrogen is a groupoid law rather than a group law. This led Heisenberg to consider an algebra of observables for this groupoid law, the so called convolution algebra for the groupoid, and it was only later that Max Born noticed that this algebra was the same as the algebra of matrices, which was very familiar in mathematics. So the groupoid interpretation vanished from the physics scene. Only now has it been revived under the influence of Connes and others.

VII. Higher dimensional groupoids

The main point I want to convey is that the simple algebra of composing arrows that we saw for a groupoid has an easy extension to higher dimensions, which was formulated by Ehresmann in the 1950s. He called it a double category, of which a special case is a double groupoid, though he had rather formal reasons for discussing them. The algebra which results may be called an algebra of squares. There are two interesting points here. One was that having convinced myself that groupoids were the appropriate tool in dimension 1, and having been educated in higher homotopy groups, it was forced on me to try to find higher homotopy groupoids, since it would have been unrealistic to suppose that groupoids were useful in dimension 1 and totally useless in higher dimensions. A second point was that the groupoid Van Kampen Theorem gave complete information in a way that seemed anomalous according to the current methods in topology. Thus there was a possibility that a higher dimensional version of the Van Kampen Theorem would open out new methods and allow for complete calculations unobtainable by other methods. The resulting theory thus fits into Kuhn's notion of scientific revolution, in terms of the analysis of an anomaly. It also fits in terms of the scientific opposition to the possibility or utility of such a theory.

A consequence of this so called "interchange law" is that there is only one way of forming a multiple composition such as that given right at the beginning in Fig 4: you may compose rows first, and then columns, or the other way round, or you can form rectangular blocks and compose each block individually before forming the final composition. This sounds simple. However, sometimes the results of such recalculations of 2-dimensional formulae are startling.

I gave earlier an argument which seemed to dash any hopes of a "higher dimensional group theory", since a "2-dimensional group" is simply a commutative group. The reason why this argument does not work for the new situation is that the squares are tagged together, and cannot move around freely as previously. This shows the difference between "products always defined" and "products defined under geometric conditions". These "double groupoids" are in a real sense "more non commutative" than are groups, and it turns out, in an extraordinary turn of fortune, that double groupoids are nicely tuned to capture the structure of 2-dimensional topology! Thus Alexandroff and Hopf are in a sense vindicated, in that the higher homotopy groups are not the "correct" structure to capture 2-dimensional topology. The "correct" objects are higher homotopy groupoids. The implications of this will take a long time to assimilate.

In order to give more of the flavour of this 2-dimensional algebra, I would like to go go back to the simple aspect, namely the role of identities, which, as I emphasised earlier, are an essential feature of the theories of groups, and of groupoids. In the 2-dimensional theory, any square has four identities, expressing that in dimension 2, there are four ways to stay still, parcelled up into the two directions you can compose squares. The edge arrows of these "stationary" squares look like Fig 52:

Figs 52a,b. Identities for squares

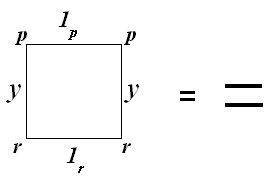where p, q and r denote vertices, and x and y denote arrows and 1_p , 1_q , 1_r are the identities. This is a rather cumbersome notation, and so we abbreviate these as shown where the lines denote identity arrows. Two of the rules for these 2-dimensional identities can then be written in the form:

But there is something else you can do in two dimensions, not allowed in dimension 1, namely make a turn, to the left or the right! This is expressed for example by a square of the form on the left below, which, in analogy with our notation for identities, we write this as on the right of the =.

We called these new elements connections, because of a relation with another part of geometry, namely parallel transport, in which the term connection occurs [9]. Contrary to what happens with identities, if you compose any of these connections with a given square, then you usually get a new square! To control this, you need laws on the connections. To see what these laws should be, it is useful to think of a connection as allowing for turning left or right, a possibility in dimension 2 but not in dimension 1. It seems reasonable that if you turn left and then right, or right and then left, then you are pointed in the same direction. This is expressed in terms of our strange symbols by the rules:

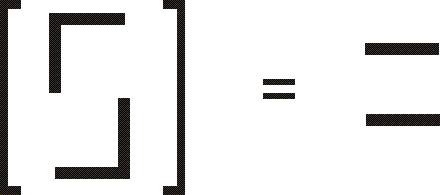This rule is in itself not quite enough for the theory. The law one really needs is called the transport law, where the left hand side might be thought of as turning left with your arm stretched out:

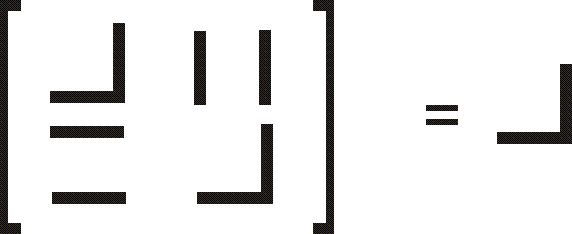Example:

A consequence of this law, and the groupoid rules, is for example, the equation on the right.

So we have a new kind of "hieroglyphic" algebra. Notice that these are calculations in dimension two. Two and higher dimensional algebra really is new and has its own concepts, which just do not appear in the easy case of dimension 1, since 1-dimensional geometry, and hence 1-dimensional algebra, is quite restricted (even boring!). The world of higher dimensional algebra is only now beginning to be explored with a strong sense of urgency and competition, as the applications, for example to physics, knot theory and computer science, are emerging.

Our new "connections" also solved one of the questions with which we started: what does it mean for one face of a cube to be a composition of the others? Since we have considered only double groupoids, we need to reduce the problem to two rather than three dimensions. There is a standard way of doing this. Take the cube, remove one face and fold the rest flat. This gives a picture as fig 55:

Fig 55. Boundary of a cube folded flat Fig 56. Composition of all but one faces of a cube

There seems to be no way of composing this because of the holes at the corners. However, when I fold the cube flat, I have duplicated the vertical edges: so the adjacent edges of each of the holes are either the same or opposite. I can now use the connections determined by these edges, and give the rule that our remaining face shall be the composition fig 56.

This is just the start of higher dimensional algebra, and the ideas above, which may seem simple, are the key tools in the proof of the the Generalised Van Kampen Theorem, due to Philip Higgins and I in dimension 2 in 1974-5. The other key input was our definition of higher homotopy groupoid, nine years after the first suggestion that these objects should exist, and 42 years after Cech's definition of higher homotopy groups. This led to the first in a series of ten joint papers, the last recently published. The Van Kampen Theorem was extended by us to all dimensions in 1977 [7]. The most difficult algebraic part is to transcribe into dimensions greater than two the ideas just described, but without getting lost in a maze of formulae. To this end, one has to avoid the above folding flat process, by using a key idea found by my research student, Keith Dakin, in 1975, namely the idea of a thin cube. This, magically, by using dimension n , enables the composition of many (n -1)-dimensional formulae, without writing down any formulae! This illustrates how a piece of mathematics can become simpler to understand in a more general framework.

A characteristic of the theory and applications is the tradeoff between the linear and the non-linear approach. The non-linear approach is the right one for the theory, and for the formulation and proofs of theorems. The linear approach is best for calculations. The translation from an obvious n -dimensional result to a linear result has yielded results to which the mathematics leads you directly, indeed they almost pop out of the page, but which, externally to the theory, are highly non-trivial. For example, when J.-L. Loday brought to the ideas developed with Higgins and myself his new models of homotopy theory, there resulted a more powerful Generalised Van Kampen Theorem [8]. This led to an entirely new construction in group theory, and so yielded calculations in topology which could not previously be formulated, let alone proved. This construction suggested analogous constructions for other algebraic situations.

Fig 57. Permutahedra

Another pursuit is that of higher order symmetry. We know that groups, and groupoids, are involved with symmetry. For groupoids the application is to what might be called variable symmetry, namely the internal symmetries of a family of objects rather than of just one object, as in the case of groups. However, higher dimensional versions of groupoids, and so of groups, exist, and have remarkable applications. It seems reasonable to suppose that there is some notion of higher order symmetry of which they are the mathematical model. Progress has been made, up to dimension 3. It would be good if these ideas were found to have physical applications, for example to fundamental particle physics, where group theory and symmetry plays such a vital role.

I have emphasised the algebra of squares and cubes, since for these objects it is easiest to see how the compositions or products work, and they give, for that reason, the easiest context in which to formulate and prove theorems. The overall aim is more ambitious, namely a general algebra of compositions, or products, of geometric objects. For example, one would like to be able to formulate what it means to compose, or form a product of, the permutahedra which form the elements of Fig 57.

The permutahedra, fig 57, is taken from a book on homotopy theory [2]. But the same picture is well known in chemistry as the structure of Zeolite! This shows the remarkable force of geometry in science. In order to form a product of the elements or pieces shown in Fig 57, there are a number of conceptual problems to solve, of the following type:

1. Define precisely the pieces of which you wish to form the product.
2.  Give the precise conditions under which the product can be formed.
3.  Under these conditions, explain how the product is defined, or computed.
4.  Give all the laws for the product.

Of all these, it seems likely that the last is the most difficult.

One solution to a range of such problems was given by David Jones in his thesis. Keith Dakin's idea of thin elements is crucial. The main point is to think of forming a product xy as constructing a triangle of the following form which might be thought of as representing a computation of this product. Laws for this product are then imposed by higher dimensional figures. Thus in this mathematical structure, geometry and algebra are inextricably linked.

The emphasis on these higher dimensional products or compositions reflects my interest in Generalised Van Kampen Theorems. The intent of such theorems is to calculate an algebraic model of a big space from the algebraic models of small parts of the space. Thus the theorem is of the type common in mathematics, and indeed in practical life, of giving procedures for relating big objects to the small standard pieces from which they are constructed. This is one reason why I feel that this type of algebra is liable to be of wide significance. The methodological aspect is that the Van Kampen Theorems require, in order to be formulated, an algebra in which compositions are of a geometric type reflecting the geometrical properties of the spaces. In particular, the algebraic objects have to have structure in a range of dimensions, since gluing in low dimensions can have strong higher dimensional implications.

You will wish to know how widespread is the knowledge and application of this theory, and where is it likely to lead. There has been a development of similar types of algebra in many places, with different aims, and with an emphasis on the theory of categories. A category is like a groupoid, except that the requirement for inverses is dropped. So categories should be useful for applications to irreversible processes, and this has been amply verified, for example in applications to computer science. The theory of categories was originally invented by Eilenberg and Mac Lane in 1945, as a way of describing some of the formal properties of mathematical theories and structures. Category Theory involves an extended analysis and development of the implications of the arrow notation for functions f :X → Y,, which came into common use in mathematics in the 1940s.

In the hands of many people, but particularly the most extraordinary mathematician of the twentieth century, Alexandre Grothendieck, Category Theory has become a tool for the invention of new languages to analyse mathematical structures and their relationships, to describe new and appropriate formulations of problems, and hence to solve classical problems. Practical tools from category theory have been used in number theory, knot theory, theoretical physics (quantum groups), computer science, and the theory of development in biology.

The theory of multiple categories is now undergoing extensive development. It is in multiple category theory, and so also multiple groupoid theory, that the problem of multiple compositions becomes a central issue. It has been handled in various ways, for example through a theory of "pastings" developed by the Australian school. The problems for multiple categories seem to be considerably more difficult than those for multiple groupoids.

VII Implications

Where are these ideas going to go? How important are they?

My own style of work runs parallel to, and interacts with, a general progress in multiple categories. This has recently had a surge of activity, with applications in several branches of mathematics, for example knot theory and low dimensional topology, and also in physics, particularly quantum groups. The ideas have been shown to be related to the formulation of a quantum field theory, and to subtle relations between knot theory and physics explained for example by Sir Michael Atiyah in [1].

Workers in computer science are also interested in multiple categories, for example in the theory of rewriting, and for investigations of concurrency. The idea in the first case is that computations are thought of as paths. There are concepts of changing one computation into another, a kind of deformation. This leads to a higher dimensional theory. In the second case, two concurrent processes are thought of as squares, which can develop in the two directions. Thus one approach to concurrency leads to a cubical approach.

One can speculate that the modelling of neurological processes requires structures more complex than the "linear" ones so widely studied in mathematics, and that algebraic objects whose definition depends heavily on geometry could be appropriate for such connectionist modelling. The story of these developments exemplifies the progress of mathematics. Here are the chain of events. Gauss studied the problem of representing a number in a particular form (in fact, x² +2xy +y²) involving two variables (x and y ). Through this he was led to the structure of commutative group. The corresponding problem for four variables finally led Brandt, about a century later, to the notion of groupoid. This notion knocked around for a number of years, and was taken up by various mathematicians for different purposes, sometimes reinventing the theory from scratch.

In 1965, I showed groupoids could be used not only for theory but also for calculation in topology. This led to the idea of developing the theory and applications of higher dimensional groupoids, using as a basis ideas of multiple category theory developed by Ehresmann for formal reasons. The change of paradigm, from groups to groupoids, was essential for the higher dimensional theory, which now has strong applications in pure mathematics and tremendous prospects. It is reasonable to suppose that higher dimensional algebra will come to bear to ordinary algebra a relation similar to the current relation of many variable calculus to one variable calculus. So the study of abstract structures, even in situations divorced from apparent "real-life" applications, has led to scientific advances and extraordinary new analogies.

It is a pleasure in this to thank all the colleagues and students who have listened to the speculations, seen what needed to be done, and have joined in getting this amazing machine up and working. The intention in this address was to show a new discipline in mathematics still in a new state, with no texts, but with a strong hold on the imagination. The intuition from which it is forged has strong links across science. But the mathematician's search for form and structure also links with the work of the artist and poet. So I hope you will like this quotation from A Midsummer's Nights Dream, since it seems to me to work also for the mathematician:

"The poet's eye, in a fine frenzy, rolling,
Doth glance from heaven to earth, from earth to heaven,
And as imagination bodies forth
The forms of things unknown, the poet's pen
Turns them to shapes, and gives to airy nothing
A local habitation and a name."

REFERENCES

1. Atiyah, Sir Michael F, The Geometry and Physics of Knots, Proc. Royal Institution, 62 (1990) 212-225.
2.  Baues, H, Geometry of loop spaces and the cobar construction, Mem. American Math. Soc., 25 (230) (1980).
3.  Brehm, U., How to build minimal polyhedral models of the Boy Surface, Math. Intell., 12 (4) 1990, 51-56.
4.  Brown, R., From groups to groupoids: a brief survey, Bull. London Math. Soc., 19 (1987) 113-134
5.  Brown, R., Elements of modern topology, McGraw Hill, 1968; Topology: a geometric account of general topology, homotopy types and the fundamental groupoid, Ellis Horwood, 1988. Republished as ´Topology and Groupoids`, Booksurge 2006. Order directly on line from the author, from Amazon etc..
6.  Brown, R., Some problems in non-abelian homological and homotopical algebra, in Homotopy theory and related topics: Proceedings Kinosaki, 1988, ed M. Mimura, Springer Lect. Notes in Math. 1418 (1990) 105-129.
7.  Brown, R. and Higgins, P.J., Colimits of relative homotopy groups, J Pure Appl. Algebra, J Pure Appl. Algebra, 22 (1981) 11-41.
8.  Brown, R. and Loday, J.-L., Van Kampen Theorems for diagrams of spaces, Topology, 26 (1987) 311-335.
9.  Brown, R. and Spencer, C. B., Double groupoids and crossed modules, Cah. Top. Geom. Diff., 17 (1976) 343-362.
10.  Connes, A., Geometrie non-commutative, InterEditions, Paris, (1990).
11.  Ferguson, H., Two theorems, two sculptures, two posters, American Math. Month. 97 (1990) 589-610.
12.  Ferris, T., The world treasury of physics, astronomy and mathematics, Little, Brown and Co., 1991.
13.  Kaufmann, L., Knots and physics, World Scientific, 1990.
14.  Robertson, S.A., Polytopes and symmetry, London Mathematical Society Lecture Notes No 90, Cambridge University Press, 1984.
15.  Robinson, J., Symbolic sculptures and tapestries, Edition Limiteé, Geneva, 1992.
16.  Wigner, E.P., The Unreasonable Effectiveness of Mathematics in the Natural Sciences, reprinted in [12].
17.  Weyl, H., Symmetry, Princeton University Press 1952.

 Top : Table of Contents.